無料ダウンロード 倍数 の 求め 方 200928-倍数の求め方 小学生
倍数算① はじめの数量の差がわかっている倍数算の解き方 倍数算ではじめの数量の差がわかっているときは、線分図がしっかりと書けていれば簡単に解けると思います。 線分図を書いて、見比べて、①にあたる数量を求めていけばよいです。小5算数 小5算数「倍数 公倍数」の問題 どこよりも簡単な解き方・求最小公倍数は小学5年生で学ぶ内容。 ただ、5年生で学ぶ場合、公倍数の求め方は、それぞれの倍数を書き出して共通する部分を探すやり方だ。 例えば、 4 の倍数 4 8 12 16 24 28 32 36 6 の倍数 6 12 18 24 30 36 9 の倍数 9 18 27 36

小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生
倍数の求め方 小学生
倍数の求め方 小学生-公倍数・最小公倍数も同様に連除法を使えば簡単かつ迅速に見つけることができます。 では具体的に見ていきましょう。 24 24 と 36 36 の公倍数を小さいものから 3 3 つ求め、最小公倍数を示せ。 連除法の手順は以下の通り。 最後に外側L字状に並んだ数字 すだれ算の使い方と 最大公約数と最小公倍数の求め方のお話です。 すだれ算 最大公約数 最小公倍数 小学生 算数 教え方 すだれ算が ちょっとだけ覚えやすくなるヒントです。 小学校5年生の算数で 最小公倍数と最大公約数という言葉を勉強します。




数学ia 整数を並べてできる3の倍数の個数を楽に求める方法 大学入試数学の考え方と解法
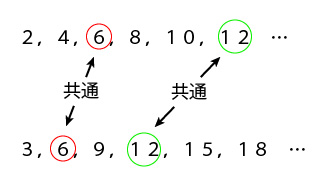
約数と倍数の発展① 最大公約数と最小公倍数の求め方(はしご算) 最大公約数と最小公倍数は、これまでのように小さい数から調べていくほかに、とても簡単な方法があります。 2つの整数を、小さい数から順にわり算をしていきます。 はしごのように見えるので「はしご算」と呼びますが場合の数と確率倍数の個数の求め方 倍数の個数の求め方 どうやったら1から100までの整数のうち, 3の倍数や5の倍数でないのかを導きだせるのかよくわからないです。 進研ゼミからの回答! こんにちは。 いただいた質問について、早速 回答させていただきます。 質問の確認 問題 ・2と3の公倍数を求めましょう。 考え方:2の段(倍数)という場所にたくさんの人(数)がいます。3の段(倍数)という場所にもたくさんの人(数)がいます。 2と3の公倍数を求めるとは 、 このたくさんの人(数)の中から 2の段(倍数)にも3の段(倍数)にもあらわれる人
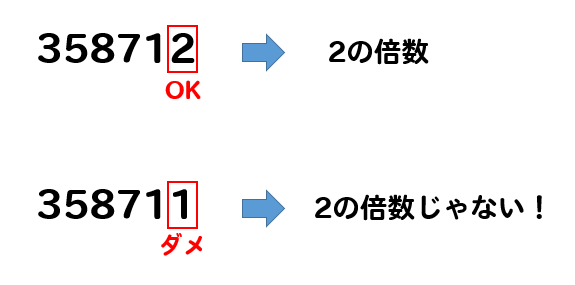
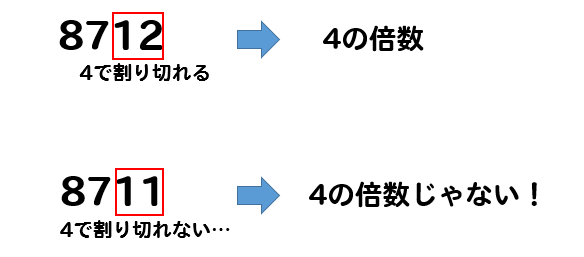
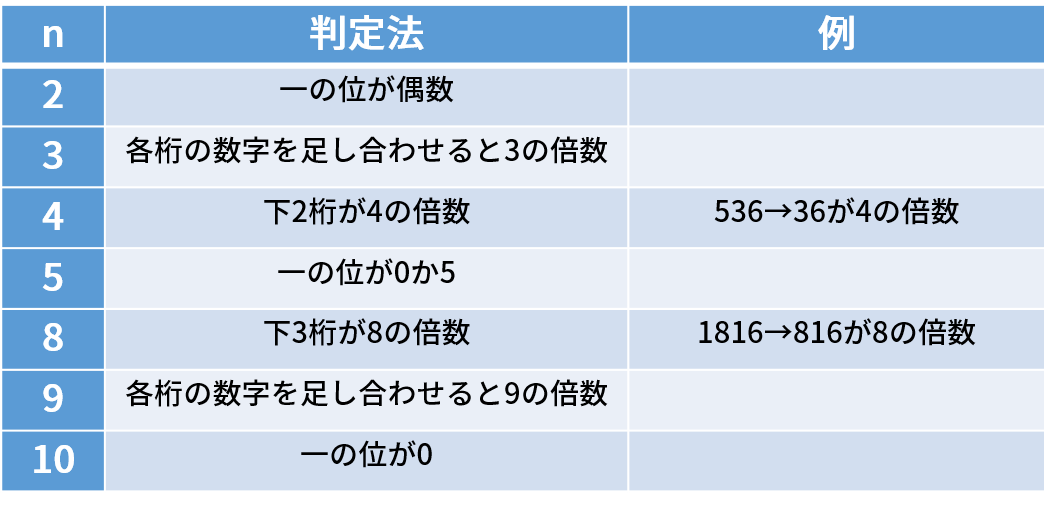
9の倍数 : 各位の数の和が9の倍数 。 例:351 など (3の倍数の例 351 は9の倍数でもある。) 他にもあるけどこれだけ知っておけば大丈夫です。 \(\,7\,\)の倍数や\(\,11\,\)の倍数などの見分け方もありますが、覚えなくて良いです。倍数算の解き方 例題1(前後の数量の和が一定) 倍数算の例題 a君とb君の所持金の比は5:4だったが、a君がb君に400円あげたら二人の所持金の比は1:2になった。a君の最初の所持金を求めよ。 a君とb君の所持金の和は変わらないので、ふたりの所持金の和を1本の数直線として、それぞれの最小公倍数(LCM)を簡単に求める計算プログラムです。 2つ以上5つまでの数を入力すると、それらの値の最小公倍数を計算して表示します。 * LCMとは、Least Common Multiple の略です。 最大5つの数に対して計算可能です
最大公約数,最小公倍数の求め方 この頁では,求め方を3通り紹介する.(中学校では,iiiは扱わない ) まず,最大公約数を次のいずれかの方法で求める. i 共通に割れるだけ割っていく方法 ii 素因数分解を利用して共通な指数を探す方法 iii ユークリッド互除法による方法 iiiでは3ケタの自然数のうち、4の倍数は、 999÷4=249 余り3 99÷4=24余り3 であるから、249-24=225 とありますが、 もし、4ケタの自然数だった場合、999 9÷4の商と、999÷4の商を、 引けば 倍数とは「ある数を整数倍した数」のこと 「0」は「偶数」ですが「2の倍数ではない」 公倍数とは「2つ以上の整数に共通な倍数」のこと 公倍数は「最小公倍数の倍数」である ホーム;




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook
の中に4がいくつあるのかが分かればOKいいので、$$\div 4=5$$よって5倍となります。 3の解説 27の中に3がいくつあるのかが分かればいいので、$$27\div 3=9$$答えは9となります。 まとめ 今回の記事は、小学4年生で習う倍の計算の仕方の教え方についてでした。 最小公倍数の求め方には、大きく分けて2つのやり方があります。 1つは、素因数分解を使う方法。 もう1つは、ユークリッドの互除法を使う方法です。 素因数分解を使った最小公倍数の求め方 たとえば、12と40の最小公倍数を求める場合は、まずは、それぞれを素因数分解します。 それぞ100までの素数についての倍数の判定法についてまとめてました。有名なものから、無理やり作ったものまで載せてあります。 倍数判定法のまとめ ↓リンク先では、証明や例まで載っています。 倍数 見分け方 2の倍数 一の位が偶数である。 3の倍数 各ケタの和が3の倍数である。




競プロ 素因数分解と約数と倍数 なかけんの数学ノート
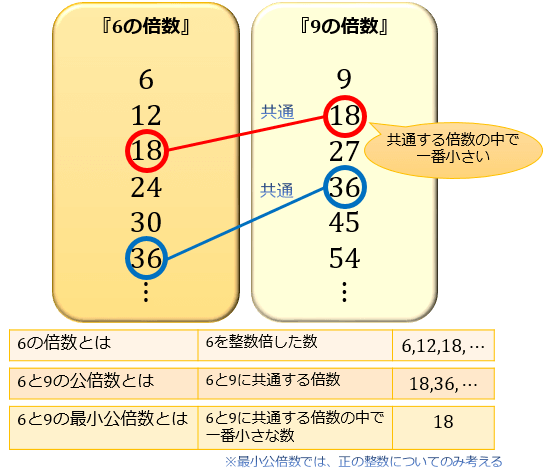



最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ
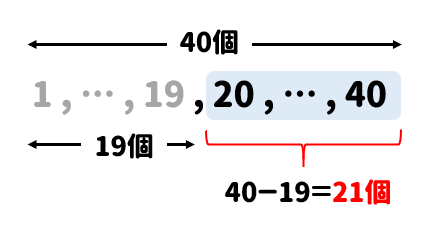
公倍数、最小公倍数の意味と求め方を理解している。 4 最小公倍数を活用する具体的な場面を考え、公倍数あるいは最小公倍数についての理解を深める。 最小公倍数の考え方を、具体的な場面で活用している。 倍数や最小公倍数を求めることができる。 5 約数の意味を理解し、求める。 約(右の求め方) ※公倍数は最小公倍数の倍数になる。 最小公倍数の求め方 例題1 次の にあてはまる数を答えなさい。 (1)72の約数は全部で 個あります。 (2)100以上の素数で3番目に小さい数は です。 (3)234、390、1040の最大公約数は です。 (4)12、40、64の最小公倍数は です。 (5)2けたの整数で今回は倍数の数え方についてパターン別に解説しました。 (1)で解説したように、個数の数え方には注意です。 ~40を数えるというときには、 「1~40」引く「1~19」というイメージを持っておきましょう。 「または」「~であるが~でない」など




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ



1
約数・倍数の計算 ツイート 約数・倍数 素因数分解 入力された値を素因数分解します。 最大公約数(2つの数) 2つの数の最大公約数を計算します。 最大公約数(3つの数② 倍数・公倍数・最小公倍数の意味と求め方 ③ 約数・公約数・最大公約数の意味と求め方 ④ 生活場面で整数の性質を使うこと 教え方1 偶数と奇数の意味と区別のしかたを教えます。 下の動画で、数には2で割り切れる数と2で割り切れない数があることを気づかせます。 動画作成協力 まず,3の倍数の見分け方を知っておこう。 3の倍数 各位の数字の和が3の倍数のとき,元の数は3の倍数である。 数学IA順列に関する問題の考え方 ここでは「順列」について説明します。順列とは,いくつかあるものを順序をつけて1列に並べる配列のことです。意味を考えて順列を
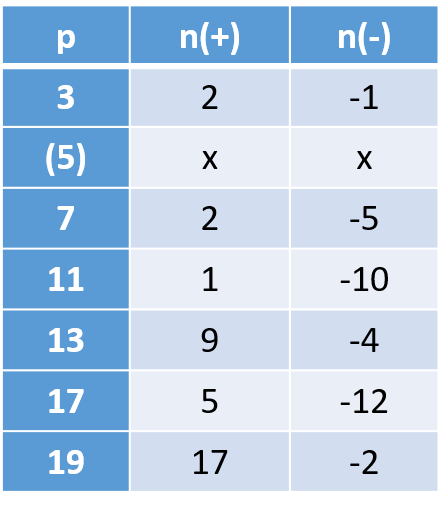



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ



Java 3の倍数や5の倍数を判定する方法 Fizzbuzz問題 ホームページ制作のサカエン Developer S Blog
公倍数と最小公倍数の求め方 ここまでの内容を理解すれば、公倍数と最小公倍数について理解できるようになります。 2つ以上の数字を比べるとき、共通する倍数を公倍数といいます。 例えば、6と8の公倍数は何でしょうか。この答えを出すためには、6と8の倍数をそれぞれ書き出してみ「指定数量の倍数」の求めることが危険物の危険性をはかるポイントになります。 指定数量の倍数(していすうりょう の ばいすう)とは、貯蔵または取り扱う「危険物の量が指定数量の何倍であるか」を表す数のことです。 求めた倍数の値によって法規制の基準が異なります。 まず、倍数の個数を求め方を説明します。「気楽に」はじめましょう 例題1 7の倍数について、以下の問いに答えよ (1)7の倍数はいくつあるか? (2)1から100の間に7の倍数はいくつあるか 小問1 7の倍数はいくつあるか? (ヒント) 気楽に考えましょう 図解 su_spoiler title="気楽に答えを見




求め方を教えてください Clearnote




最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ
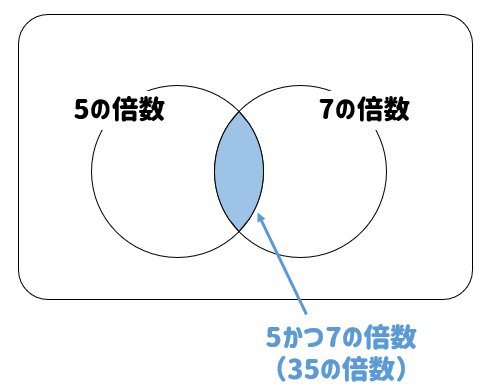
100以下の自然数のうち2の倍数かつ5の倍数の求め方を教えてください。 高校数学 東映系の映画がTOHO(東宝?)シネマコンプレックスで公開されるのは何故ですか? 映画 将来スポーツの大会を企画する職業に就くためには文系か文理系どちらへ進むべきでしょうか? 私は文系の高2です 3 簡単計算二等辺三角形の高さの求め方がわかる3ステップ 中1数学 中学数学「円の面積の求め方」の公式を1発で覚えてしまう裏技 中2数学 1575 3分でわかる!小数をふくむ連立方程式の解き方 中2数学「100以下の自然数のうち、3の倍数または5の倍数の個数」などの求め方を解説するよ。ポイントを確認しよう。 point 注目すべきなのは、 「かつ」 、 「または」 という表現だよ。 「2の倍数 かつ 3の倍数」というのは、 (2の倍数)∩(3の倍数) ということ。つまり、 「2の倍数と3の倍数の共通部分




倍数算は4つの出題タイプの解法を覚えよう 恋する中学受験 大学受験を見据えた中学受験




小5 算数 小5 18 倍数と公倍数 Youtube
7の倍数・13の倍数の見分け方(おまけ) $7$ の倍数判定法と $13$ の倍数判定法は、作るのが結構めんどくさいです。 桁が大きい場合 以下の二つの式 \begin{align}1001=7×11×13 \ , \ =3^3×7×11×13×37 ④\end{align} を利用して、$3$ 桁ずつに区切って考える。 桁が小さい場合 「一の位とそれ以外 ここで、最小公倍数の求め方を一つ紹介します 言葉で書いてもわかりにくいので先ほどの24と36の例で見てみましょう。 素数は2と3が登場しています。2については3乗、3については2乗が最大ですね。 よって最小公倍数は より72だとわかります。 素因数分解のやり方に不安がある人は
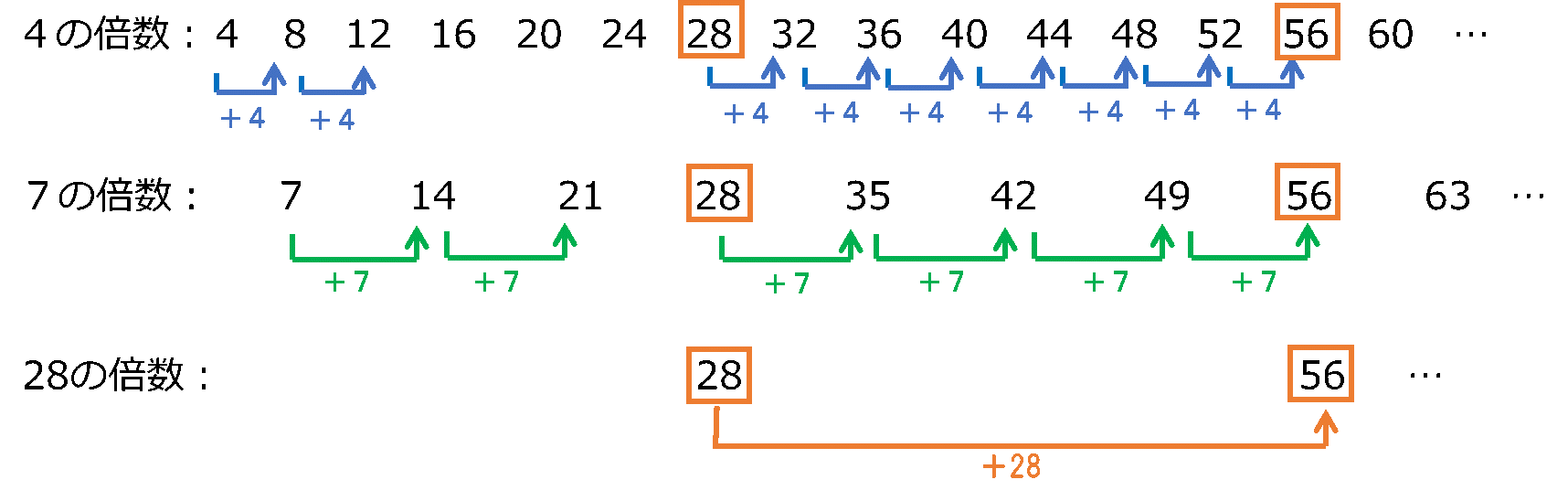



倍数と約数の教え方 5 倍数 公倍数の実践問題 ママのための受験算数の教え方プチ講座 中学受験ナビ



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




倍数とは 意味と求め方を学ぼう 算数パラダイス
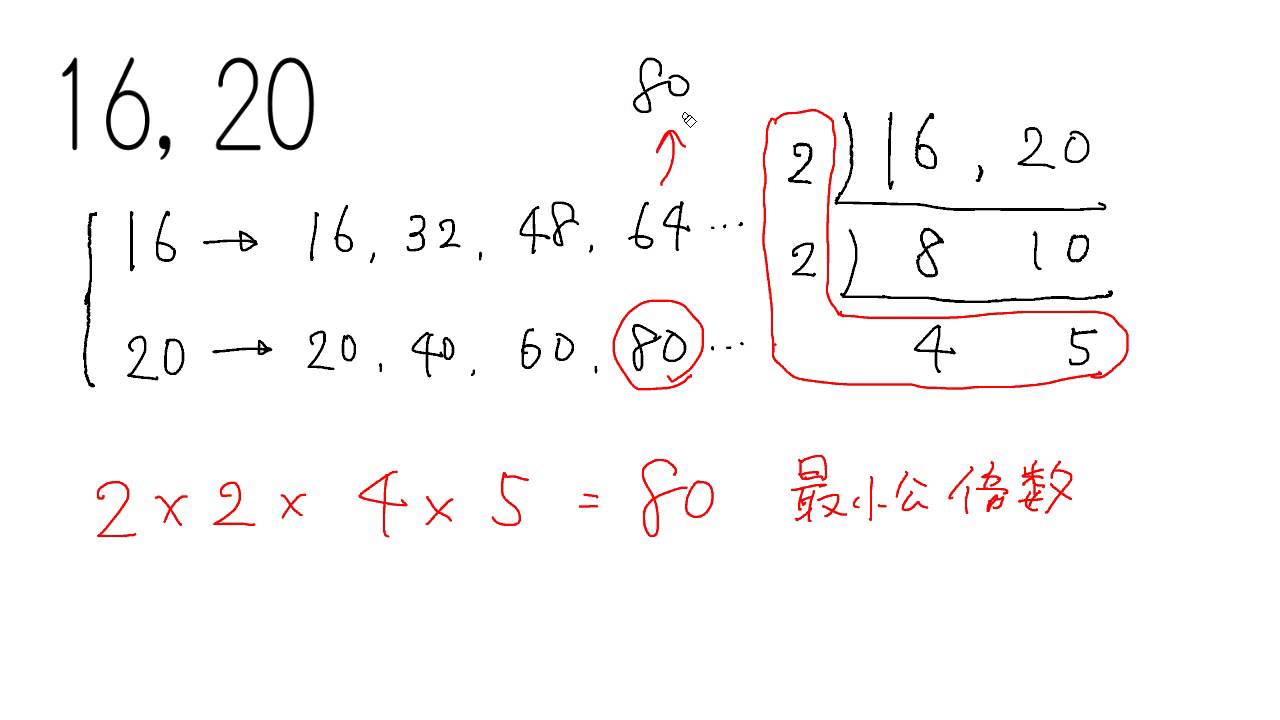



大きな数の最小公倍数の求め方 Youtube




倍数判定法まとめ 3の倍数 4の倍数 7の倍数などの見分け方とは 遊ぶ数学




知らないと受験で損をする 倍数の見分け方とカード並べの問題での使い方 中学受験ナビ
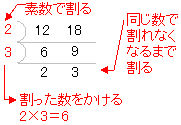



約数 倍数




高校数学a 倍数の個数1 かつ または 例題編 映像授業のtry It トライイット
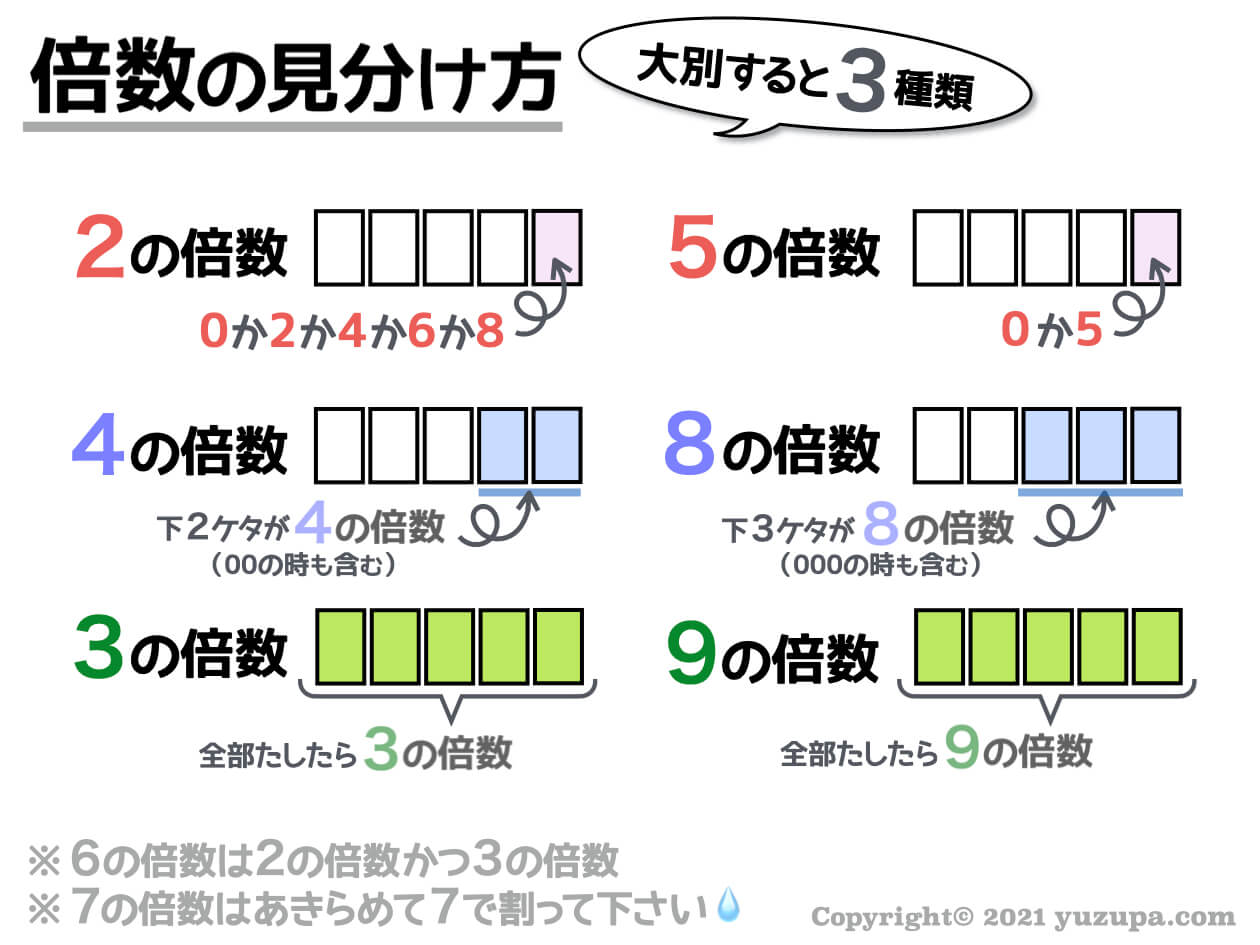



中学受験 倍数の見分け方 3種類の見分け方を使いこなせ かるび勉強部屋
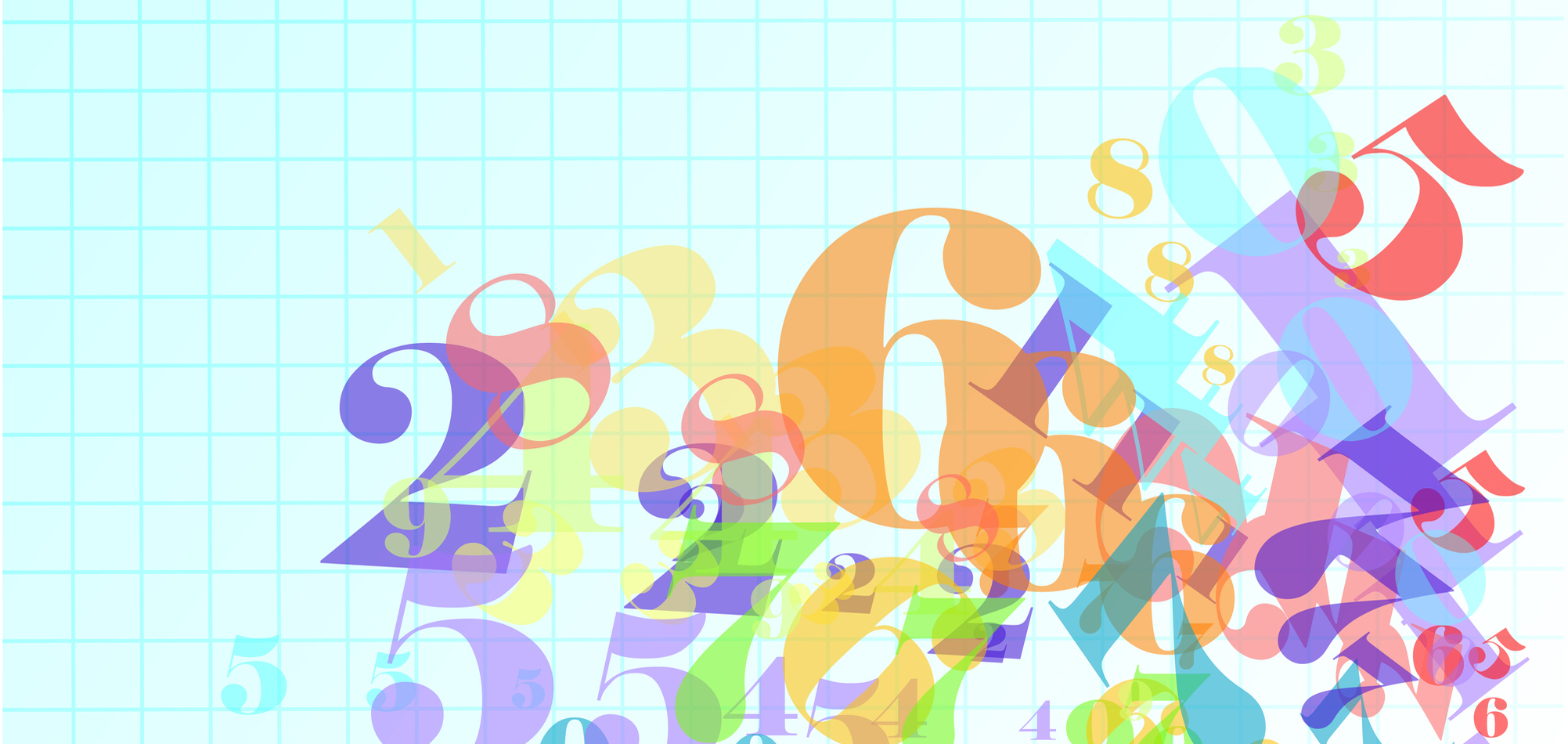



倍数とはどのような数ですか 用語の区別と最小公倍数の求め方に慣れよう 中学受験ナビ




数学ia 整数を並べてできる3の倍数の個数を楽に求める方法 大学入試数学の考え方と解法




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




約数と倍数 小学算数の最大公約数と最小公倍数の求め方 リョースケ大学




倍数とは 意味と求め方を学ぼう 算数パラダイス



乙4危険物の指定数量の倍率計算を習得しよう Uhiyamabumi



倍数 公倍数の求め方 もう一度やり直しの算数 数学
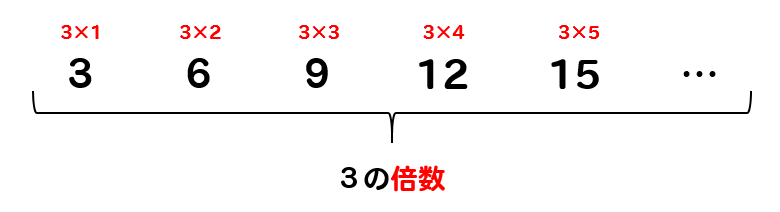



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ



3
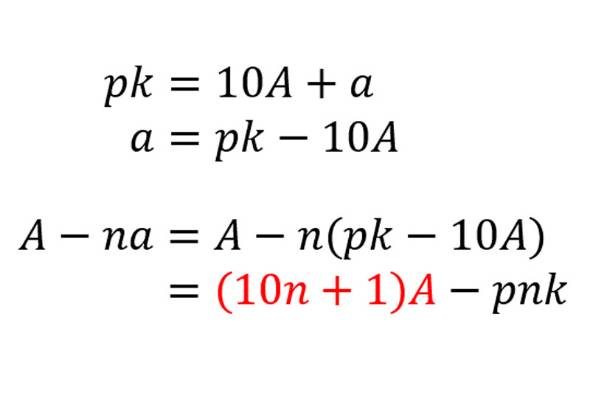



ある数が の倍数か を見分けるための 万能 な方法 ねとらぼ




11のかけ算 11の倍数 のわかりやすい計算方法 Irohabook
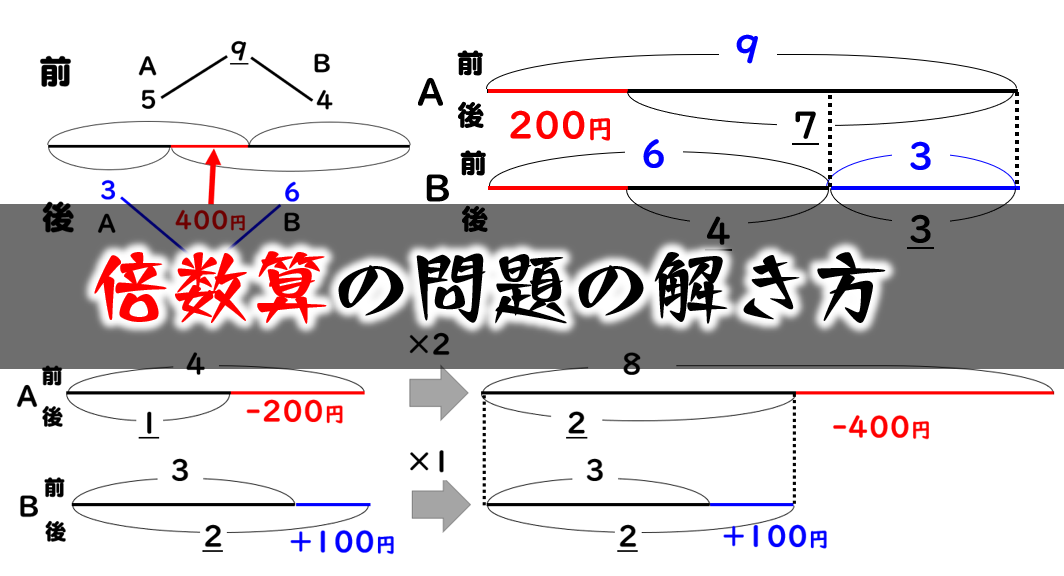



倍数算 の解き方とポイント 3つのパターンを数直線で解説 数学fun




小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




は7の倍数 7の倍数判定法 前編 Youtube
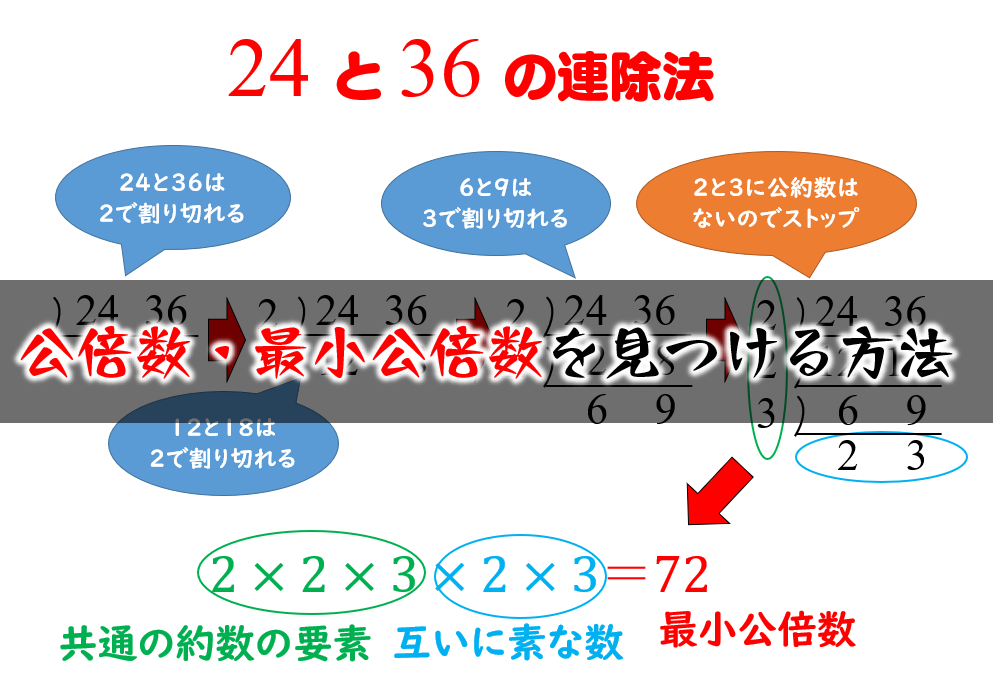



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
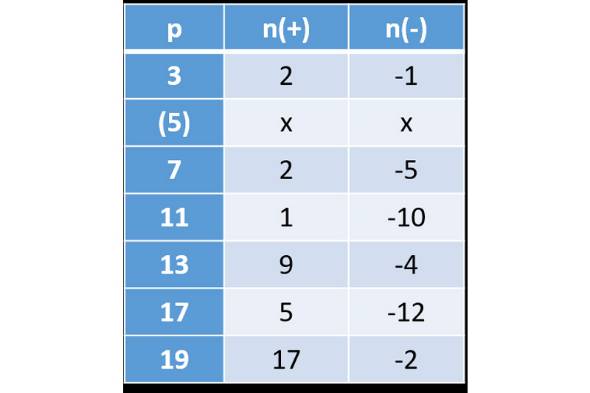



ある数が の倍数か を見分けるための 万能 な方法 ねとらぼ




2 13の倍数の判定法をまとめ 簡単な倍数の見分け方
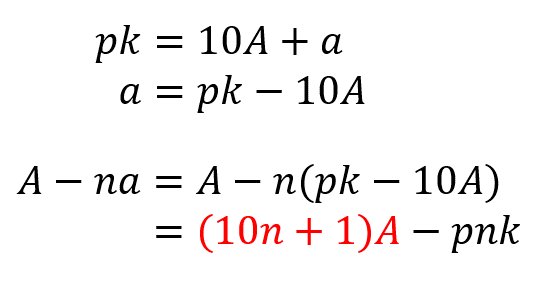



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




塾長ブログ 倍数の見つけ方




4 1が解説見ても分からないです Clearnote
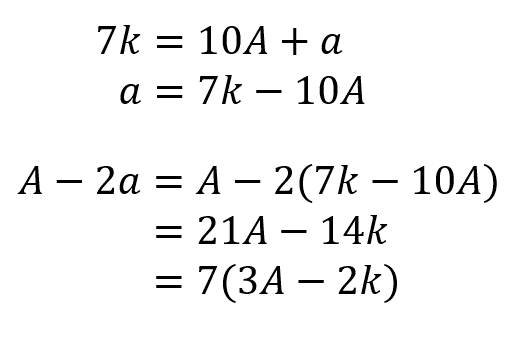



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




倍数の個数を求める問題 どうやって考えればいい 数スタ




3と4の最小公倍数は 3と5の最小公倍数は 3と4と5の最小公倍数は ウルトラフリーダム




知らないと受験で損をする 倍数の見分け方とカード並べの問題での使い方 中学受験ナビ
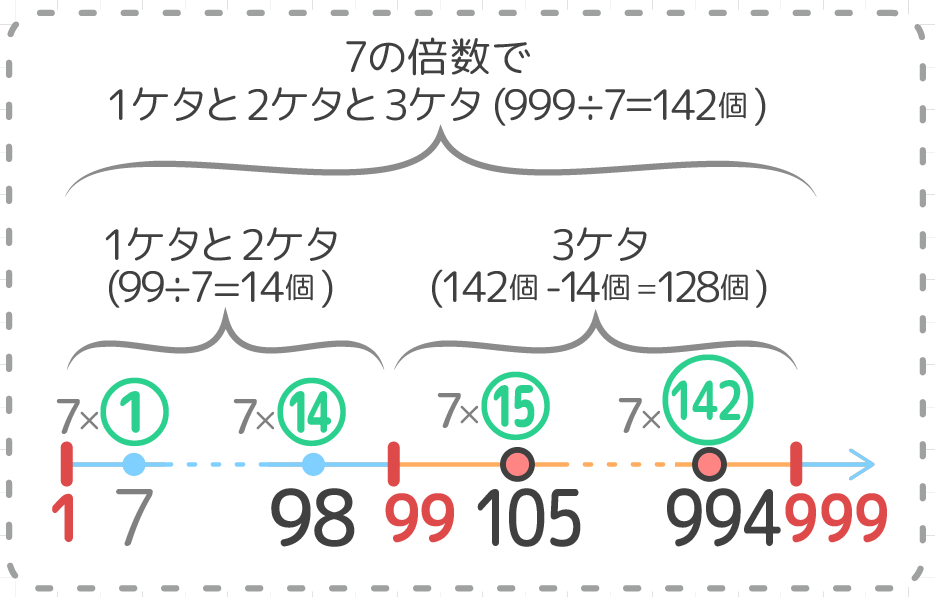



小学生 倍数の個数の求め方 2ケタ 3ケタ等 中学受験頻出 そうちゃ式 受験算数 新1号館 数論 特殊算




最小公倍数の求め方とは 数字が何個あっても計算できるやり方をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



3




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



倍数の個数を求める問題 どうやって考えればいい 数スタ




小学生 倍数の見分け方は 三 四 六 九などの分かりやすい判定法 そうちゃ式 受験算数 新1号館 数論 特殊算




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support




高校数学a 3と9 4と8 6と12 7と11と13の倍数 余り の判定法 受験の月



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




中学受験算数 超便利 倍数の見分け方知ってる 算数お役立ちテクニック1 Youtube




4の倍数 8の倍数になるような数字とは 例えばなんですか Clearnote




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算




エがわかりません どうやって考えてますか 総和の出し方がわかりません Clearnote




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




小5 算数 小5 倍数 公倍数 最小公倍数 Youtube
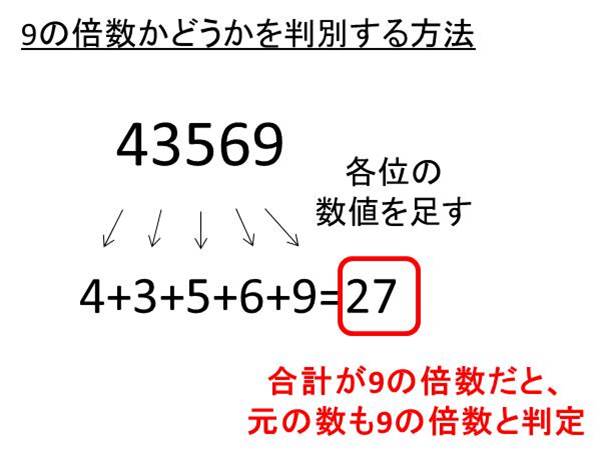



9の倍数の判別方法 各位の和から見分ける 白丸くん




エがわかりません どうやって考えてますか 総和の出し方がわかりません Clearnote
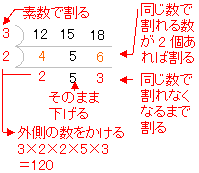



約数 倍数
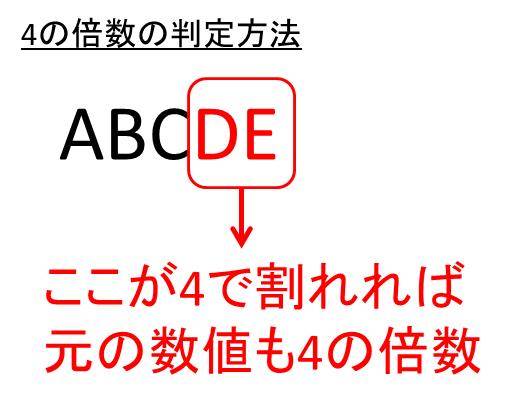



4の倍数の判定方法とその証明 見分け方 白丸くん
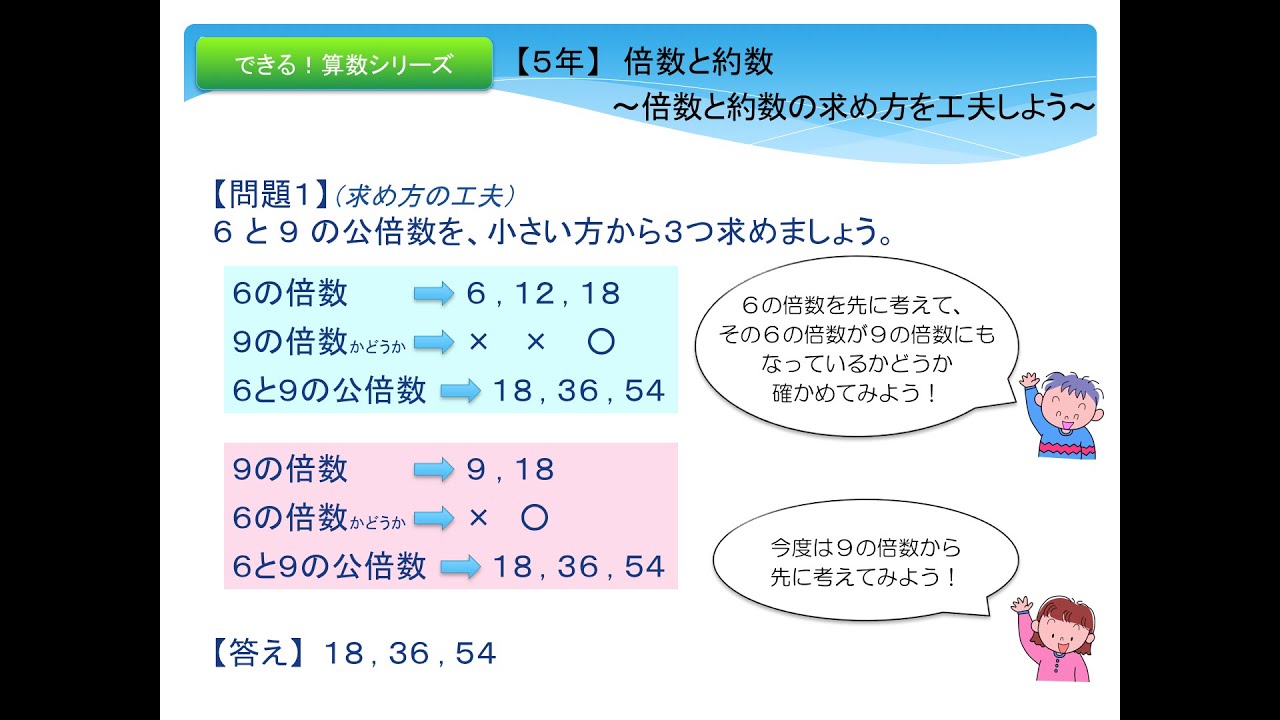



スマホok 5年 倍数と約数 倍数と約数の求め方を工夫しよう Youtube




高校数学a 3の倍数 9の倍数の見分け方 映像授業のtry It トライイット




1からp Kまでの自然数のうち Pの倍数の個数の求め方を教えてください Clearnote




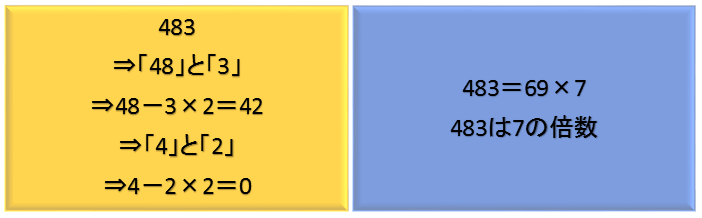
これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ




の倍数は何通りできるか問題 数学の偏差値を上げて合格を目指す



Studydoctor約数 倍数とは その求め方 Studydoctor




倍数とは 倍数の見分け方 ぐらたん塾




これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




倍数 約数 算数用語集




小5 倍数の意味 日本語版 Youtube




高校数学a 倍数の個数1 かつ または 映像授業のtry It トライイット



これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ




中学数学 整数 3の倍数 3の倍数の見分け方 理由 オンライン無料塾 ターンナップ Youtube



倍数の個数を求める問題 どうやって考えればいい 数スタ
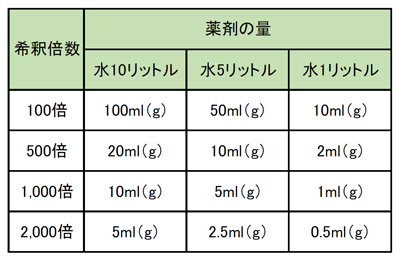



農薬の希釈 きしゃく 倍数とは Ja西春日井




高校数学b 等差数列を利用する倍数の和 受験の月




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




小学校5年 算数 公倍数の求め方 Youtube




4の倍数かつ6の倍数 4の倍数であるが6の倍数でない数 5の倍数であるが7の倍数でない数 などの求め方 100以下の自然数 ウルトラフリーダム
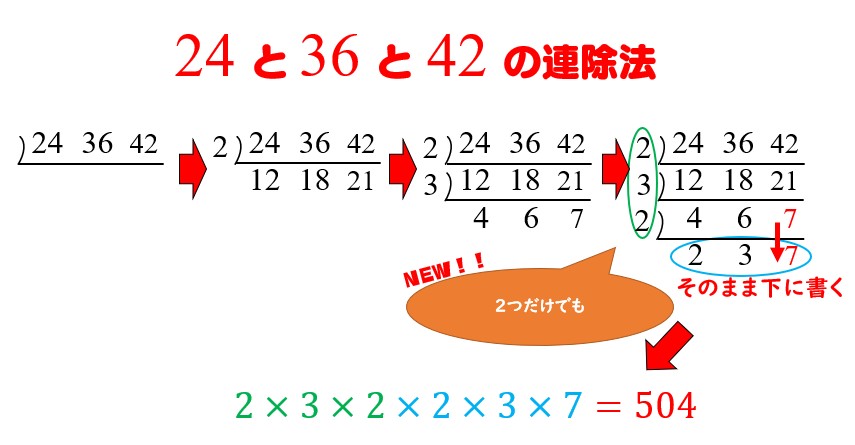



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




高校数学a 倍数の個数1 かつ または 練習編 映像授業のtry It トライイット



倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



倍数 公倍数 最小公倍数 通分 分数のたし算ひき算の授業 教材 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
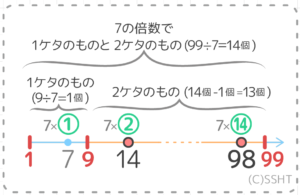



小学生 倍数の個数の求め方 2ケタ 3ケタ等 中学受験頻出 そうちゃ式 受験算数 新1号館 数論 特殊算




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook




高校数学a 4の倍数 8の倍数の見分け方 映像授業のtry It トライイット




ある数が の倍数か を見分けるための 万能 な方法 ねとらぼ



3



数学 順列について 3の倍数の4桁を作るとき 各位の和が3の倍数 Yahoo 知恵袋



5年算数整数 偶数奇数公倍数公約数 教え方




1から100までの整数のうち3の倍数は何個 1から100までの整数のうち6の倍数は何個 1から100までの整数のうち2で割り切れるが3で割り切れない数は何個 ウルトラフリーダム




プログラミング 数学 特定条件の数は何個 Scratch Yuyu Log




1番のy 0 5まではいけたのですが その後3の倍数の求め方なんですが Clearnote




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook
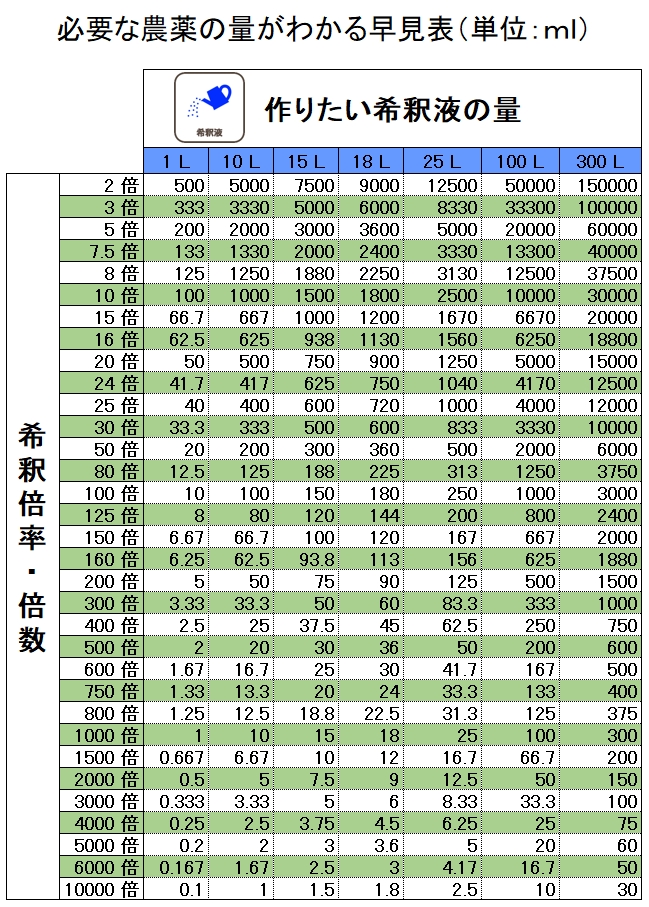



図解でわかる農薬の希釈倍率 倍数と早見表 計算方法と注意点も解説
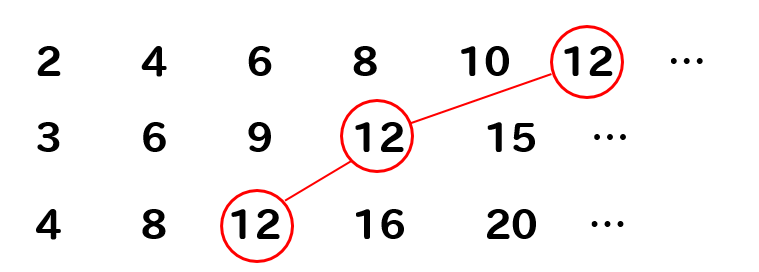



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ



6の倍数の求め方を教えてください Yahoo 知恵袋

No comments: